Zu Chongzhi Mathematics Research Seminar
Date and Time (China standard time): Monday, October 9, 10:00-11:00 am
Location: WDR 1007
Zoom: 944 9590 2163; Passcode: dkumath
Title: De Giorgi’s conjectures about second-order elliptic equations and their connections to regularity of weak solutions to a natural network formation model
Speaker: Xiangsheng Xu
Bio: Dr. Xiangsheng Xu is currently a professor of mathematics at Mississippi State University. He received his B.S. degree from Nanjing University in 1982 and his Ph.D. in mathematics from the University of Texas at Austin in 1988. After spending two years at Texas A&M University as a visiting assistant professor upon his graduation, he accepted a tenure-track position at the University of Arkansas in 1990. He left there to join Mississippi State University in 1995 and has stayed there ever since. Over the years, he has also payed short term visits to many institutions around the world. Semester-long visits include Northwestern University in 1998, Rutgers University in 2002, and Duke University in 2015. His main scientific contributions are in the areas of mathematical analysis of electrical heating of conductors (the so-called thermistor problem), crystal surface growth, and many others.
Abstract:
In 1995, De Giorgi gave a lecture in Lecce, Italy on the continuity of weak solutions to second-order elliptic equations of the form
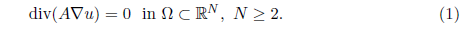
He conjectured about the optimal conditions on the coefficient matrix A = A(x) under which weak solutions of the above equation stay continuous. It turned out that regularity properties of weak solutions to a natural network formation model would be consequences of these conjectures if one also knew how continuous these weak solutions were. We can prove this in the two dimensional case and the high dimensional cases remain open.

