Zu Chongzhi Center Mathematics Research Seminar
Date and Time (China standard time): Friday, December 16, 10:00-11:00 am
Zoom ID: 982 3269 9841
Passcode: dkumath
Title: Random band matrices and Anderson’s conjecture in high dimensions
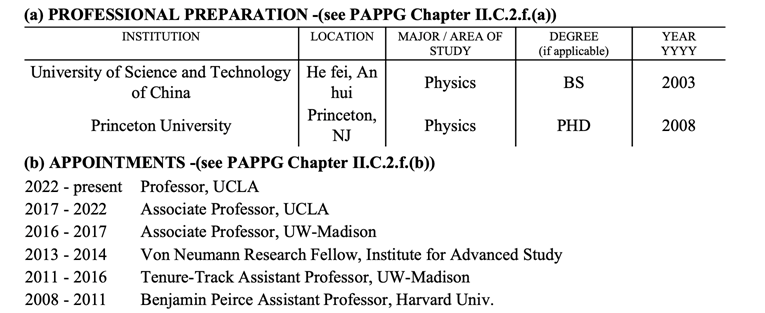
Speaker: Jun Yin
Bio: Jun Yin received a Ph.D. degree in Physics from Princeton University in 2008. He is now a Professor of Mathematics at the University of California, Los Angeles.
Abstract: One famous conjecture in quantum chaos and random matrix theory is the so-called phase transition conjecture of random band matrices. It predicts that the eigenvectors’ localization-delocalization transition occurs at some critical bandwidth $\mathrm{W}_{\mathrm{c}}(\mathrm{d})$, which depends on the dimension $\mathrm{d}$. The well-known Anderson model and Anderson conjecture have a similar phenomenon. It is widely believed that $W_c(d)$ matches $1 / \lambda_c(d)$ in the Anderson conjecture, where $\lambda_c(d)$ is the critical coupling constant. Furthermore, this random matrix eigenvector phase transition coincides with the local eigenvalue statistics phase transition, which matches the Bohigas-Giannoni-Schmit conjecture in quantum chaos theory. We proved the eigenvector’s delocalization property for most of the general $d>=7$ random band matrix as long as the size of this random matrix does not grow faster than its bandwidth polynomially. In other words, delocalization occurs as long as bandwidth $\mathrm{W}$ is larger than $L \varepsilon$, for matrix size $L$, and some $\varepsilon>0$. It is joint work with H.T. Yau (Harvard), C.J. Xu (Harvard), and F. Yang (Upenn).

